MS Excel 로 최소제곱법을 활용한 직선 그리기
Microsoft Excel 에서 데이터를 활용하여 그래프를 그리고, 최소제곱법을 활용하여 데이터에 대해 가장 맞는 직선을 그리는 방법에 대해 다룹니다.
최소제곱법을 활용한 가장 맞는 직선을 구하는 방법 (피팅)에 대한 자세한 내용은 다른 포스트에서 설명하고 있습니다. (Link)
그래프 그리기
무엇이든 그래프를 그리려면, 데이터가 있어야 합니다. 그래프를 그린다는 것은 데이터를 두 개 이상의 좌표축을 가지는 어떤 좌표 평면 상(또는 공간, 그 이상)에 위치하도록 하는 것이니요. \(i\) 번째 데이터를 \(x_i\), \(y_i\) 로 생각하고, 다음과 같은 데이터가 있다고 합시다.
이 데이터는 \(x_i\) 의 순서에 따라 정렬되어있으나 원칙적으로는 정렬되어있을 필요 는 없습니다.
| \(i\) | \(x_i\) | \(y_i\) |
|---|---|---|
| 1 | 1 | 5 |
| 2 | 2 | 11 |
| 3 | 3 | 15 |
| 4 | 4 | 13 |
| 5 | 5 | 18 |
| 6 | 6 | 22 |
| 7 | 7 | 24 |
위 표의 \(x_i\) 와 \(y_i\) 를 이용하여, 데이터포인트를 그래프 위에 찍어보도록 합니다.
- 일단 엑셀을 켜고
제일 중요함 -
다음 그림과 같이 데이터를 표 형태로 입력합니다. (맨 왼쪽의 \(i\) 세트열은 입력하지 않아도 됩니다.)
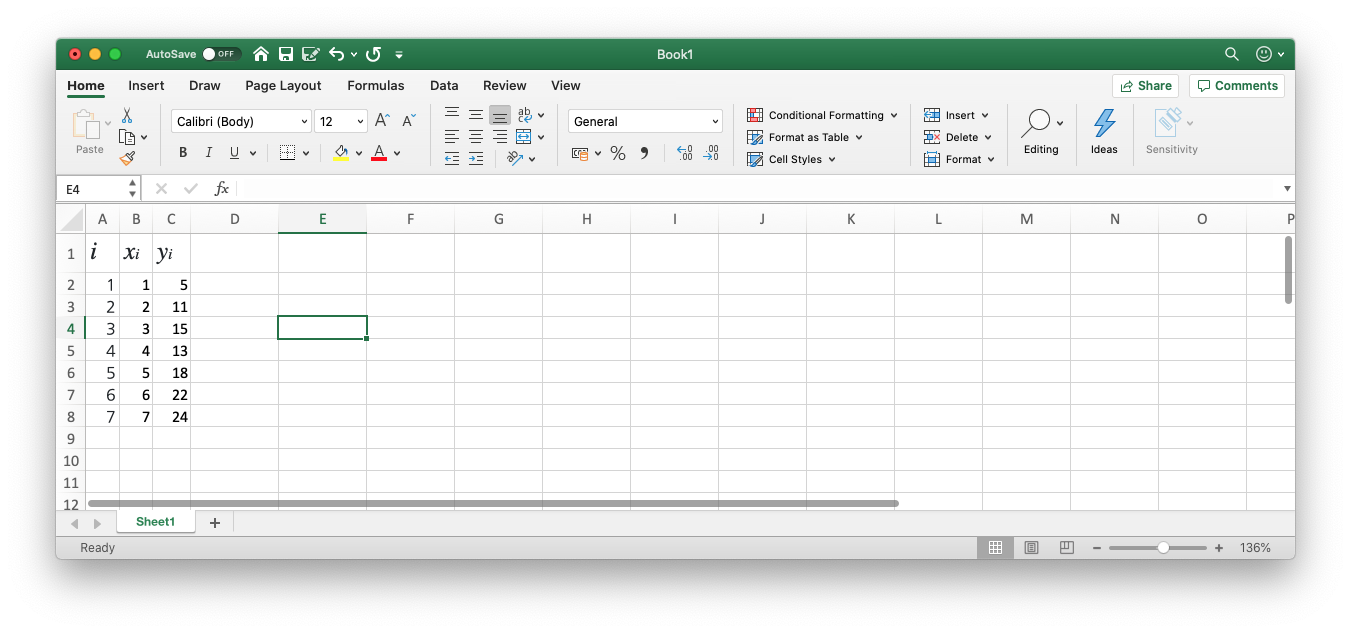
-
그래프를 그릴 데이터포인트 X,Y 를 한번에 드래그하여 선택하고, 상단 바에서 삽입(Insert) 을 클릭한 이후, Recommended Charts (권장 차트?) 옆의 여러 차트들 중 가로 세로 축 사이에 점들이 몇개 찍혀있는 버튼을 클릭한 이후, 분산형 그래프 분류의 선 없이 점만 찍혀있는 그래프를 선택합니다.
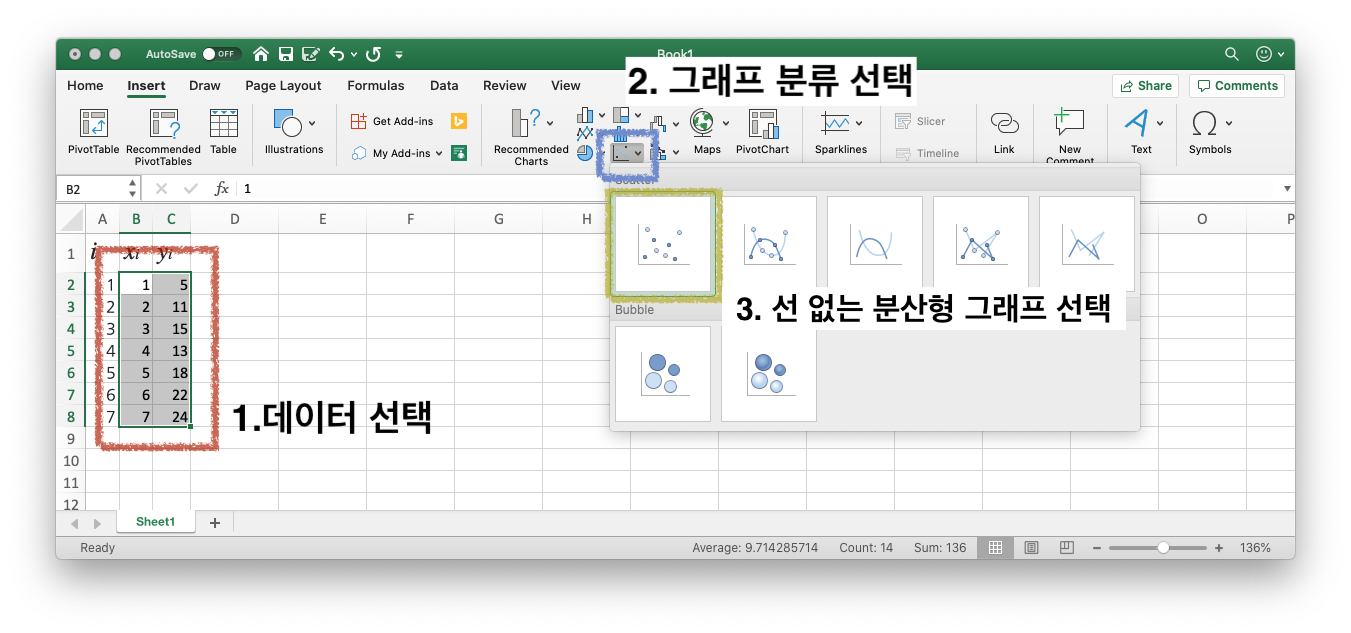
-
그러면 아래 그림과 같이 데이터를 기반으로 그래프가 그려집니다.
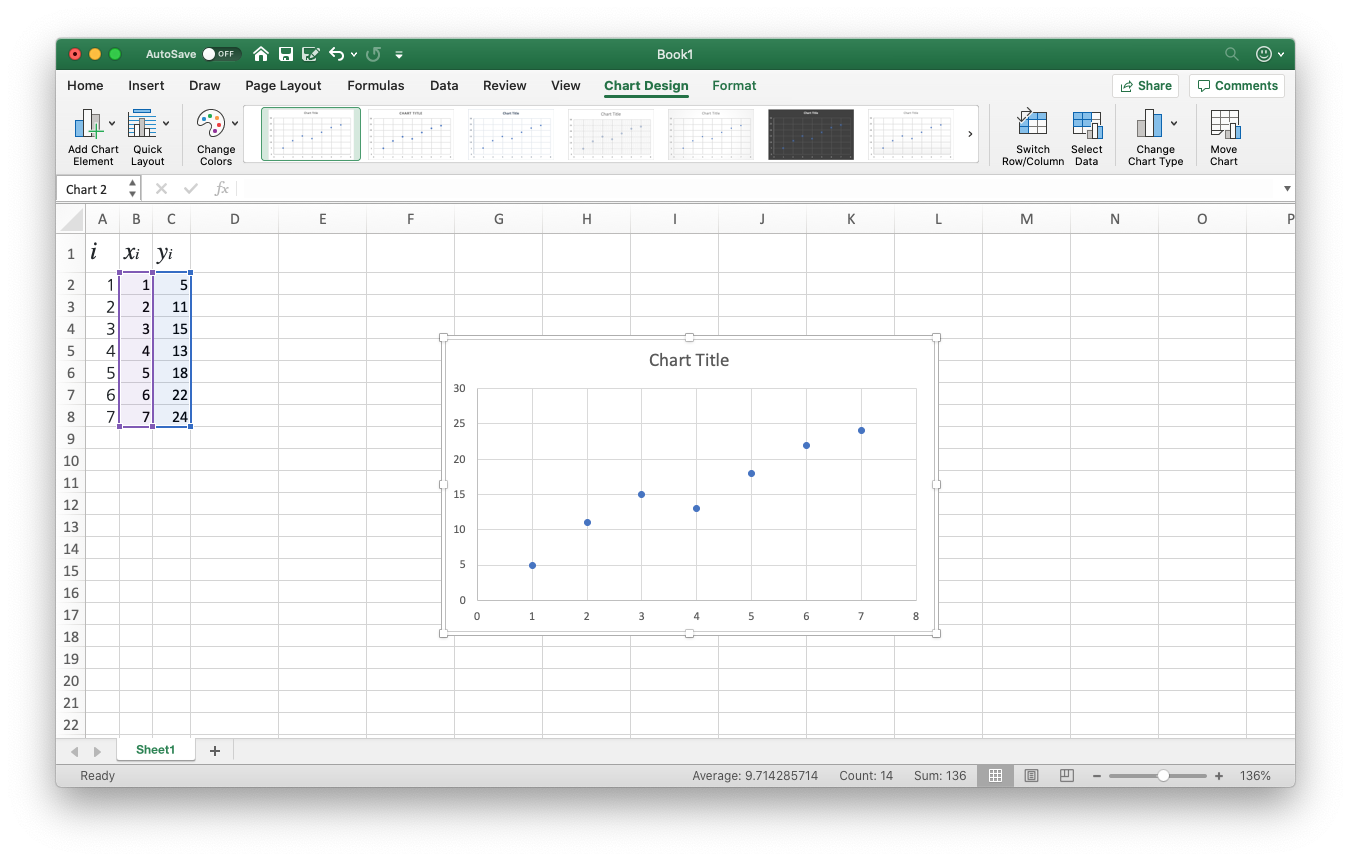
- 참고로, 축 이름이나 단위는 따로 표기해줘야 하는데, 알아서 찾아보길 바랍니다.
조금만 둘러보면 있음
그래프 위에 최소제곱법을 이용한 직선식 그리기
최소제곱법을 활용하여 그래프를 그리기 위해 일반물리학실험실 총괄 홈페이지link 에 업로드된 최소제곱법 엑셀 시트link나, 손으로 구하는 수식을 쓰는 것은 매우 노가다스러운 측면이 있습니다. 하지만, 엑셀 (또는 한컴오피스, macOS 넘버스, MATLAB, Mathematica, SPSS 등 데이터 분석을 조금이라도 끼고 있는 소프트웨어는 다 있음.) 에는 기본적으로 수식을 구해주는 기능과 직선식 플로팅 기능이 있습니다.
다음과 같이 안내해드리니, 유용하게 활용하세요.
-
(그려진 그래프에서) 그래프의 데이터 포인트 점에 마우스 커서를 대고 한번 클릭하면, 아래와 같이 데이터포인트 전체가 선택됩니다.
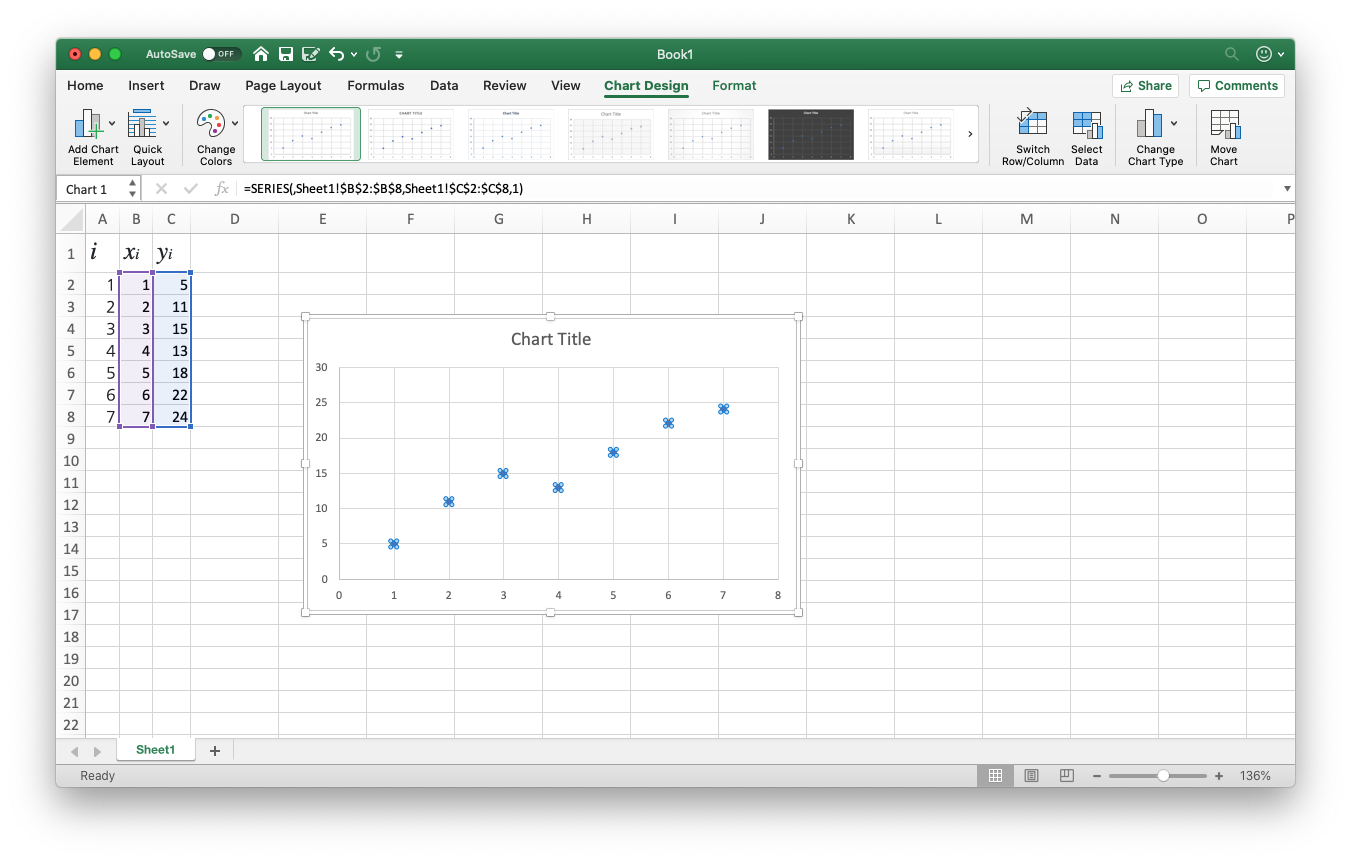
-
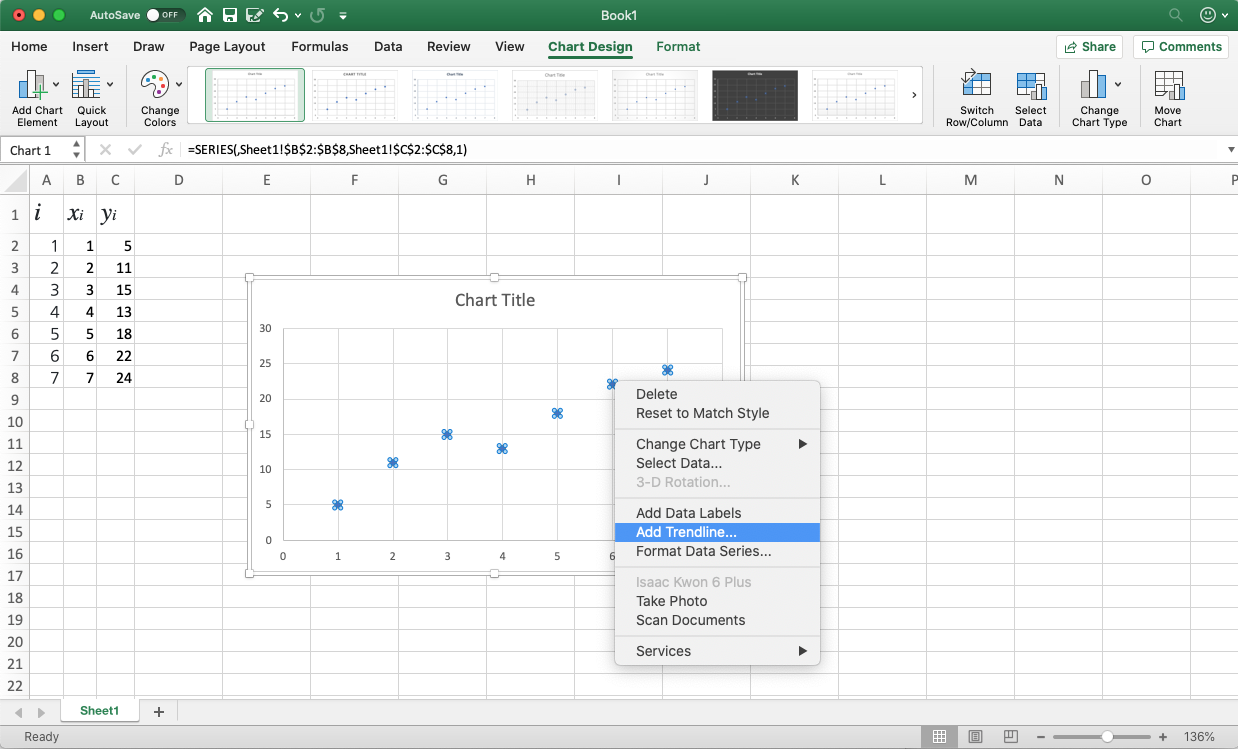
선택된 그 이후, 그 포인트 위에서 오른쪽 클릭을 하면, 드롭다운 메뉴가 뜹니다. 거기서 Add Trendline (추세선 추가) 를 클릭합니다.
-
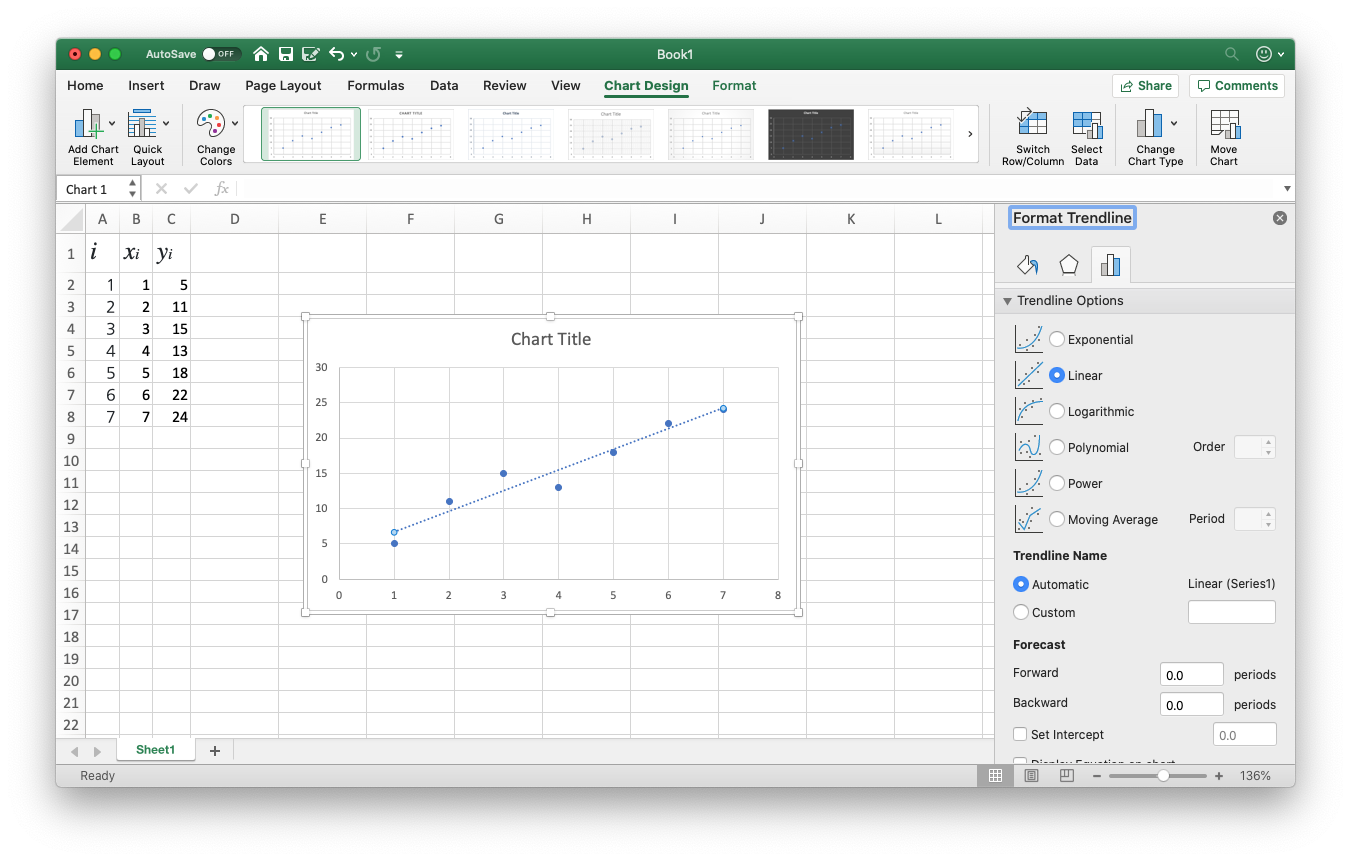
이게 최소제곱법으로 구한게 맞는진 아직 모르겠지만뭔가 직선이 추가되었습니다!
-
그 이후 오른쪽에 뜨는 차트 디자인 메뉴를 밑으로 내려보면 “Display Equation on chart (차트에 방정식 표시)” 와 “Display R-square value on chart (차트에 R² 표시)” 가 있습니다. 체크해주면, 그래프에 방정식과 R² (결정계수) 가 표시됩니다.
결정계수가 뭔지는 알아서 찾아보쇼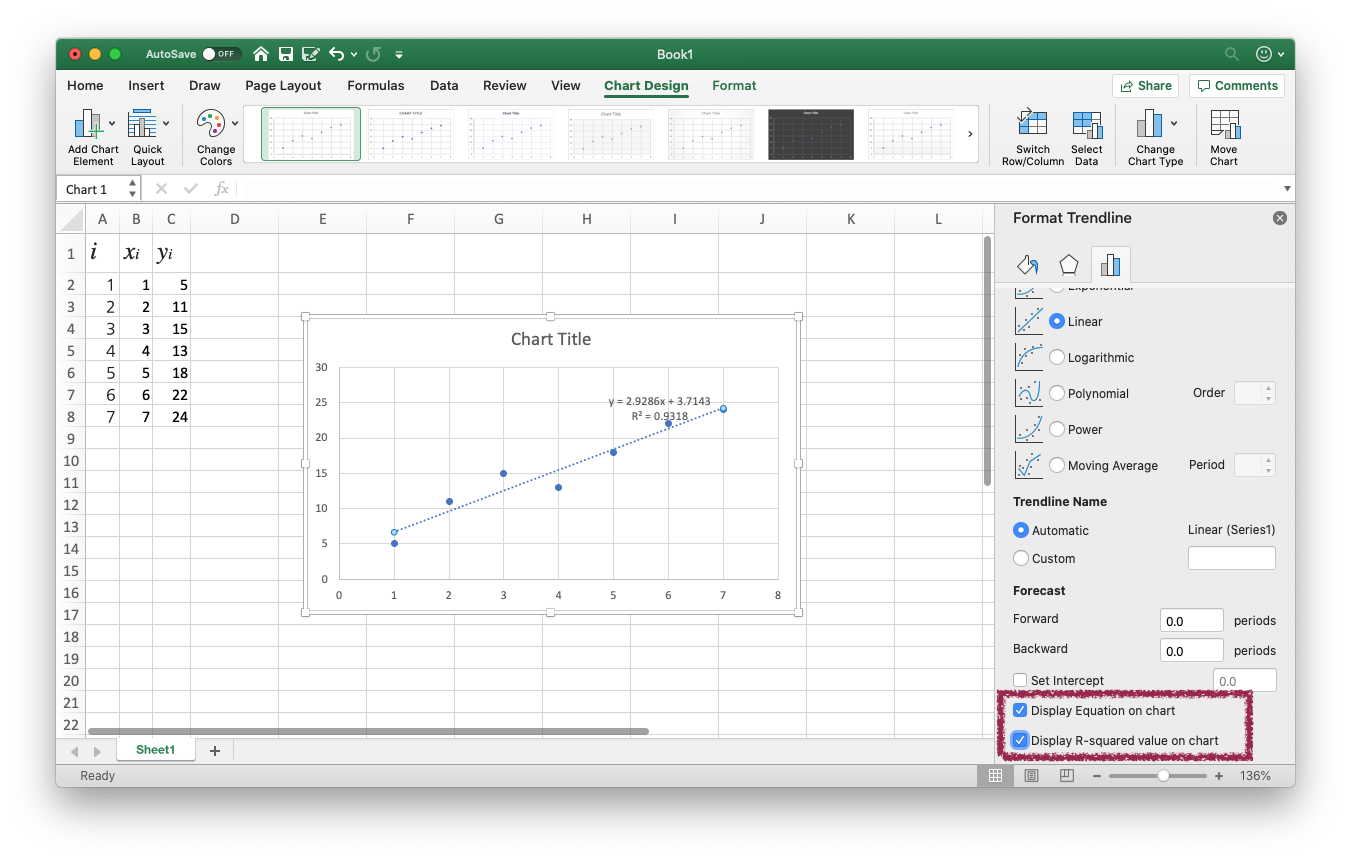
-
만약, 이게 최소제곱법으로 구한게 맞는지 의심된다면, 따로 한번 더 구해서 저 수식과 비교해보면 됩니다.
그런데 아무도 안해보겠지
데이터포인트를 설명하는 직선식에서 계수의 정확한 값, 불확도, 통계량 구하기
Q: 그런데, 직선 식 다 구했는데 직선식에 그 불확도 안구해주니까 그 뻘짓은 또 해야하는 것 아닌지요?
A:아이고 불확도 구할거라는 생각만 해도 장하다아뇨. 사실 저 그래프의 계수들을 구해주는 함수는 따로 있고 그걸 그래프에서 끌어쓴 다음 일부분만 그림에서 보여주는거라 그 과정 전부의 통계치를 구하는 함수인 LINEST 를 쓰면 편안합니다.
LINEST 함수
자세한 건 Excel 의 LINEST 함수를 따로 찾아보셔도 되지만 (한글판 설명서, 영어판 설명서), 일단 설명만 드리면, 여러 변수에 대해 Linear 한 함수로 Estimation 하는겁니다. n(n>2)개의 변수열에 대해 서로간의 관계를 선형식으로 예측하는 방법입니다.
그래서, 2차원 축을 가지는 평면의 점에서 직선을 찾거나, 3차원 축의 공간에서 평면의 수식에 대한 계수 (등 n 차원 공간에 대해 n-1 차원 요소의 계수) 를 찾습니다.
=LINEST(Y열, X열, TRUE, TRUE)
로 수식을 한 칸에 입력해주면, 연달아서 여러 값이 생겨납니다.
$C$2:$C$8 과 $B$2:$B$8 을 일일히 입력해줄 필요는 없고, =LINEST( 까지 입력한 다음에 데이터 범위를 마우스로 긁어주면 (수식을 입력하던걸 취소하지 말고 긁어주면 자동으로 범위가 입력됩니다.)됩니다. 한 범위를 입력하고, 콤마를 찍은 후 다음 범위를 선택하고 엔터를 치면 됩니다.
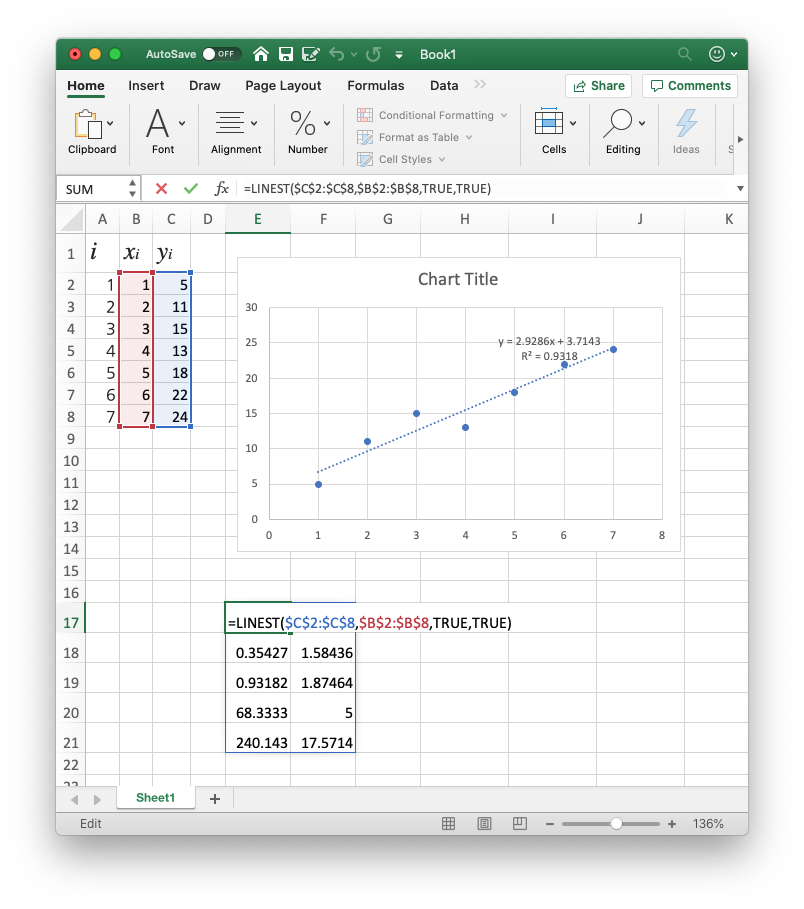
자, 그러면 이제 저기에 생긴 숫자들이 뭘까요…?
숫자를 봐서는… 맨 위 두 숫자가 계수를 뜻하는건 아주 잘 알겠고, 위에서 세번째 왼쪽 것이 R² 인것도 알겠어요. 나머지는 뭘까요…?
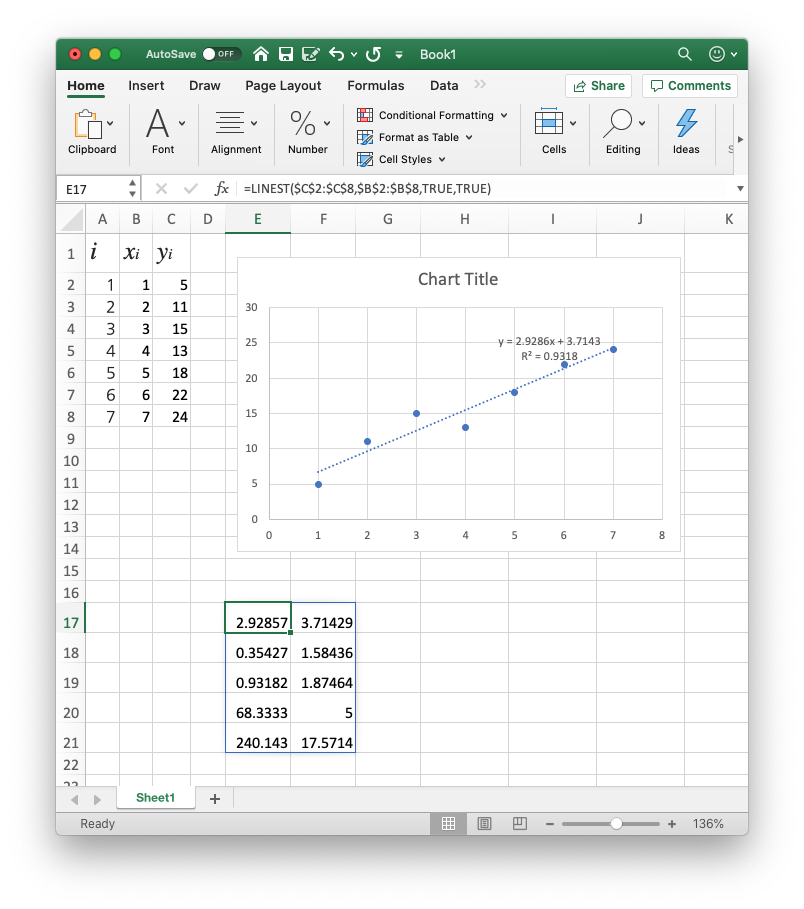
이럴땐 매뉴얼을 보면 됩니다.

위에서부터, 각 행은 다음과 같은 의미입니다.
- 추정된 계수
- 본 데이터에서 계수가 2개만 나온 것은, \(y=ax+b\) 피팅이어서, \(a\) 와 \(b\)가 나온 것입니다.
- \(n=2\) 이 넘는 다변수통계를 쓰면 (\(z=ax+by+c\) 등) 그 이후 계수도 구할 수 있습니다.
- 각 계수의 불확도
- 결정통계량
- R²
- y 추정의 총괄 표준오차
- 검수통계량
- F통계량 (찾아봐요, 딱히 필요하진 않음)
- df (Degree of Freedom) : 포인트 갯수가 7개이고, 계수가 2개라 자유도가 5입니다. 자유도가 0보다 작으면 피팅이 불가합니다.
- 거리통계량
- 회귀제곱합 (딱히 불필요)
- 잔차제곱합(이걸 최소화하는걸 찾는 방법)
네. 이런 방법으로 좀 더 편하게 계수들을 찾을 수 있습니다. 우리 모두 ‘노가다 해서 힘들어할 시간’ 에 결과에 대한 탐구를 더 하면 됩니다.
그래서 이걸 어디다가 쓰면 되나요?
아이고 다 쓸모없는 짓이었네툴이 뭘 뜻하는질 모르면 쓰지를 맙시다
직선 식 추정은 계수를 구하기 위해 하는 것입니다. (다른 포스트 참고: Link)
이론에 의해 예측된 수식의 개형이 직선일 때 그 계수를 구하거나, 또는 종속변수가 독립변수에 대해 선형으로 비례한다는 것을 보이고 싶을 때 (\(R^2\) 통계치, \(\chi^2/\mathrm{ndf}\) 로) 사용합니다. 일반물리실험의 보고서에서는, 데이터 간 관계를 수식으로 규명할 수 있을 시 반드시 써야합니다.
당연히 예측된 수식의 개형은 직선이 아닐 수 있습니다. 대부분의 예측형은 직선으로 재변환이 가능합니다만, 굳이 귀찮게 몇몇 수식은 그러지 않아도 됩니다. Excel 에는 데이터 분산이 없는 최소제곱법에 대해, Trivial Solution 이 있는 몇몇 수식 개형은 최소제곱법 수식 계산을 지원합니다.
Excel 에서 지원하는 최소제곱법 (2021.04.13)
- 선형 - linear
\(y=ax+b\) - n차 다항식 - nth polynomial
\(y=\sum_{i=0}^{n} a_i x^i\) - 지수 함수 - exponential function
\(y=a e^{bx}\) - 로그 함수 - logarithm
\(y=a \ln^{x} + b\) - 멱함수 - power function
\(y=a x^b\)
선형 함수의 LINEST 를 제외하고는 사실상 셀 함수 형태의 숫자 계산은 내장되어있지 않다고 해도 무방합니다만, 실험 통계를 조금 배워보시면 LINEST 만으로 다른 모든 함수 개형도 계수를 계산할수 있음을 알 수 있을겁니다. (여기서 따로 다루지는 않겠습니다.)
Trivial Solution 이 없는 경우의 최소제곱법의 활용
예를 들면, \(y=Ae^{bx}+C\) 은 물리학에서는 아주 일반적인 수식인데도 엑셀에서 곧바로 피팅을 할 수 없습니다. 그러면 어떻게 해야할까요?
- 개노가다
- 일단, \(y=a e^{bx}\) 는 지원하니까, 모든 \(y_i\) 에서 같은 숫자 \(C\) 를 빼고, \(y=a e^{bx}\) 로 피팅하면 될겁니다.
- \(R^2\) 이 피팅이 잘 되었는지나 그렇지 않은지를 판정해주니, 그것만 보고 손으로 잘 \(C\)를 정해주면 됩니다.
(뭐?)
- 노가다는 싫다
- 그렇습니다. 세상 사람들이 그렇게 멍청하지는 않습니다. 선지자는 아주 좋은 방법을 잘 마련해두었습니다.
- MATLAB, Origin, Numpy(Python), ROOT(C++) 등 다른 프로그램을 쓰세요.
제발 메소드는 고생말고 사서 드세요 - Non-Linear Chi-Square Minimization 이라는 방법인데
말 그대로임경사하강 등의 수치 해석적 최소화 방법을 씁니다.
그래프 그리고도 욕먹는 경우 감점당하는 경우
그래프를 고생해서 그렸지만, 다음 경우에는 그 그래프가 오히려 감점 요인이 될 수 있습니다.
- 그래프에 활용한 데이터 간 절대 관계가 없을 경우.
- 실험원리상 관련이 있거나,
- 실험 분석에서 관련이 있음을 기술하면 해야 함.
- 그래프를 그리는 이유가 있어야 함
- 최소제곱법에 활용한 수식 개형이 잘못되었을 시
- 예1) Exponential 의 함수 개형 \((y=Ae^{bx}+C)\)을 써야하나, 선형\((y=ax+b)\)를 썼을 경우
- 예2) \(y=ax^2+bx+c\) 의 2차 함수 개형으로 충분하나, \(y=ax^6+bx^5+~\dddot~+g\) 와 같이 불필요하게 많은 계수를 적용한 경우
- 파라메터 4개면 코끼리도 그립니다. paper link 그림 출처
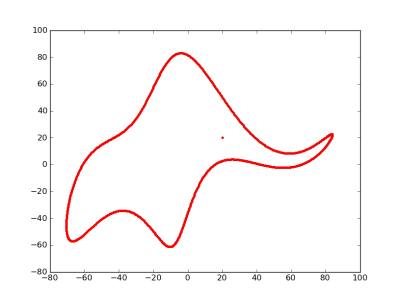
아뇨 하나면 되는데paper link그림 출처

- 파라메터 4개면 코끼리도 그립니다. paper link 그림 출처
