측정과 통계

본 포스트에선, 측정을 진행하고 그 측정 결과를 다시 실험결과로 받아들이기 위한 통계적 과정과, 각 통계요소가 가지는 의미에 대해 알아봅니다.

측정의 가장 간단한 예시인 “길이 측정” 을 기본으로 하며 “동전의 지름 측정” 을 예시로 들었습니다.

세 줄 요약

알아들을 수 있을리 만무하지만, 일단 세줄 요약을 먼저 전달드립니다.

1. 측정은 어떤 모분포를 기반으로 유한한 갯수의 표본을 뽑아내는 것이다.
2. 뽑아낸 표본을 기반으로 다시 모분포를 추정해야, 실제로 세상이 말하고자 하는 바를 알 수 있다.
3. 추정된 모분포의 성질을 추론하기 위한 것 또한 표본만으로 진행해야하나, 그 값이 참값을 정확하게 추정하는데에는 노력이 필요하다.

그래서, 이런 말도 해볼 수 있습니다.

신은 모르겠고 나는 주사위 놀이를 한다.

실험

실험은, 어떤 독립변수_{Independent Variable}와 종속변수_{Dependent Variable} 관계를 규명하기 위해 진행하는 것으로, 가설의 설정과 그 가설에 대한 증명 으로 이루어집니다.

독립변수와 종속변수의 관계를 규명하려면, 당연히 그 독립변수와 종속변수를 어떻게 측정하여 수치화할 것인지에 대한 문제부터 답해야 합니다. 아니, 자로 재면 길이가 나오고, 스톱워치로 재면 숫자로 딱 시간이 나오는게 아니라고요? 맞긴 한데, 내재된 오차의 형성 과정이…

측정의 의미 : 아날로그와 디지털

측정이란 아날로그를 디지털로 바꾸어 수치화하는 것으로서, 전혀 기록되지 않은 어떤 현상을 기록하는 것입니다.
일상생활에서 볼 수 있는 모든 현상은 아날로그로 취급할 수 있으며, 그 현상을 특정 기구에 의해 수치화되어 기록하면 디지털이 됩니다. (여기서의 아날로그 는 참값 이라는 말로, 디지털 은 측정값 이라고 부르기도 합니다.)

주변에 있는 여러 요소들을 위 기준으로 아날로그와 디지털로 나눠보면 다음과 같습니다.

• 아날로그
  • 어떤 물체
    • 물체의 길이, 몸무게 등
  • 어딘가에서 시작된 소리에 의해 생긴 마이크의 떨림
  • 전등에서 나온 불빛
• 디지털
  • 어떤 물체의 길이 측정값
    • 사람의 키 측정값
  • 어떤 물체의 무게 측정값
    • 어떤 사람의 몸무게 측정값
  • 마이크의 떨림을 수치화하여 기록된 시간당 떨림값 (전류, 또는 떨린 길이의 시각당 측정값)
    • 음악 파일로 기록된 음악 참고: 레코드판, 카세트테이프에 저장된 소리 는 아날로그임.
  • 전등에서 나온 불빛을 수광다이오드로 받아 측정된 광전자의 갯수 측정값
    • 사진 파일 (컴퓨터나 휴대전화에 저장된)
      참고: 필름 카메라로 찍은 사진 은 아날로그임.

측정값에 적용되어있는 오차

아날로그를 디지털로 바꾸는 것은 정해진 측정 방법에 의해 어떤 디지털 값을 정하는 것으로, 그 측정 방법은 당연히 측정 값에 영향을 줍니다. 측정 방법이 어떻게 되느냐에 따라 값은 참값이라도 다르게 측정할 수 있고, 측정값 자체가 달라질 수 있습니다. 당연히, 두개 이상의 측정자, 측정 척도, 측정 방법이 있는 경우 값의 신뢰성을 위해 교정_Calibration 이 있습니다만, 서로 다른 과정 측정과정은 결국 서로 다른 오차의 형성을 가져올 수 있습니다.

본 장에서는, 어떠한 참값으로부터 오차가 어떻게 측정 기기를 거쳐 측정값에 영향을 미칠 수 있는지에 대해 알아봅니다.

시스템에 의한 오차

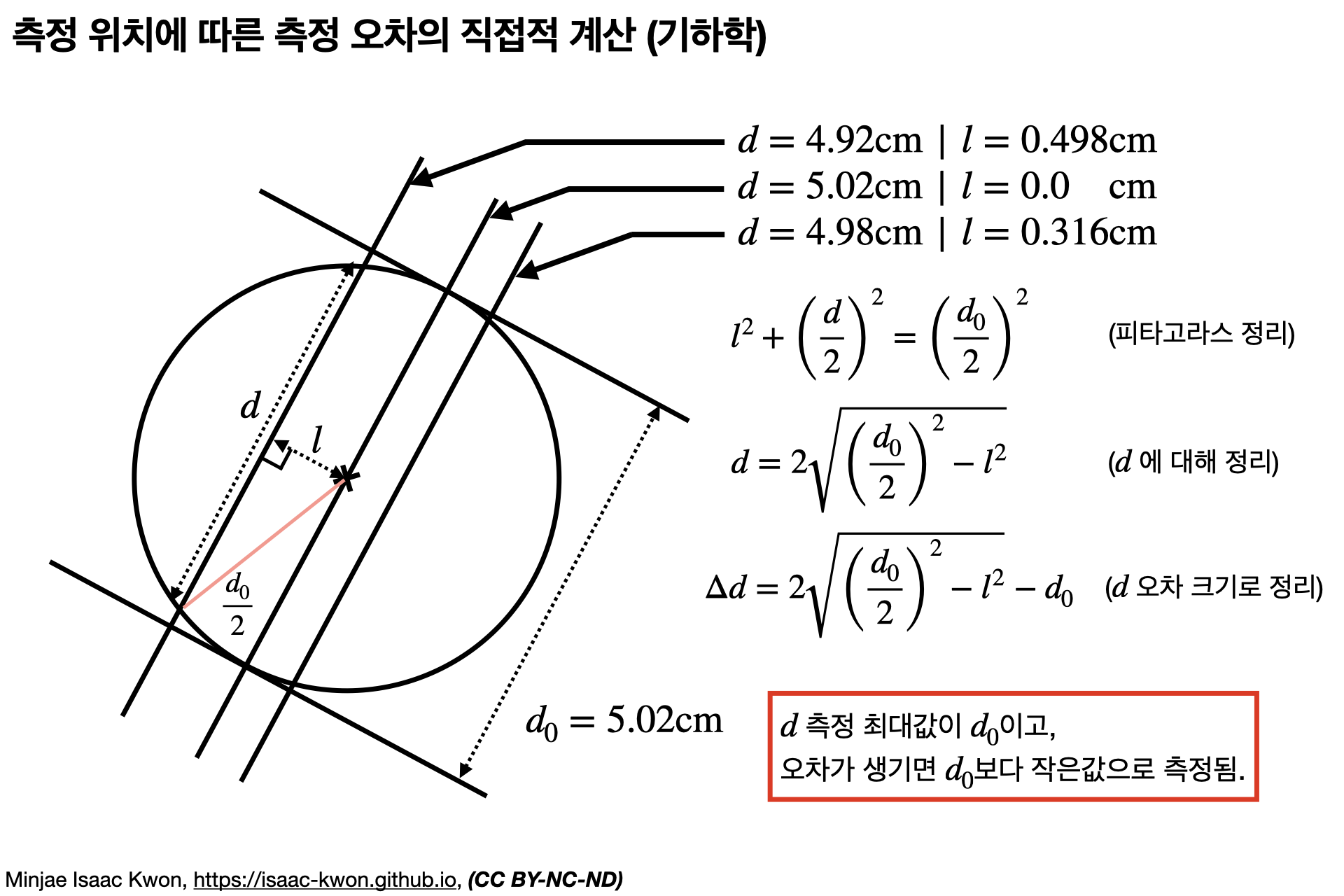
동전의 지름을 측정한다고 합시다. 다만, 계산의 편의를 위해 지름의 참값이 정확하게 \(5.02\mathrm{cm}\) 이라고 합시다.

동전의 지름을 \(15\mathrm{cm}\) 자와 같은 일반적인, \(0.1\mathrm{cm}\)간격 눈금자로 측정한다고 할 때, 여러 오차가 적용될 수 있습니다. 대표적인 오차로, 동전의 중심점을 통과하도록 하지 못하는 것이 있습니다. 정확하게 그 점을 통과할 리는 당연히 없으니, 당연히 발생해야만 하는 오차이기도 합니다. (점은 면적이 0이므로, 당연히 평면 위에서 점과 직선이 교차할 확률도 0)

동전을 완벽한 원을 밑면으로 하는 원기둥이라고 가정하면, 윗면의 원의 지름 \(d_0\)을 측정할 때 원과 자의 측정선과의 거리 \(l\)에 따라 지름의 측정값에 오차 \(\Delta d\)가 얼마나 발생할 지 기하학을 활용하여 다음 그림과 같이 바로 계산할 수 있습니다.

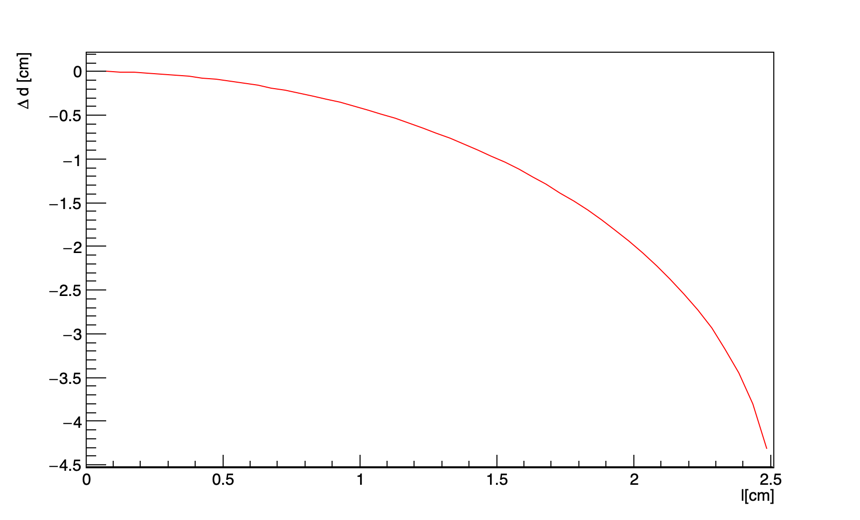
그래프는, 위에서 계산된 \(l\)에 따른 \(\Delta d\) 의 변화 를 그래프로 그린 것입니다. \(l\)이 반지름인 \(2.51 \mathrm{cm}\) 을 넘는 경우의 \(\Delta d\) 는 정의되지 못하며 (수식으로 풀면 복소수로 나옴.) \(l=0\) 에서 절대값이 최소이고, \(l\) 이 증가함에 따라 절대값이 단조 증가하는 (직관적으로 자명한) 사실이 그대로 그래프에 드러납니다.

이 오차는 \(l\) 을 정확하게 알면 \(\Delta d\) 를 완벽하게 계산할 수 있지만, 당연히 측정자는 \(l=0\) 으로 믿는 지점에 측정자에 놓을 것이므로 그러는 것은 불가능합니다. 과학적 측정을 하려면, 어떻게든 이런 것도 분석해내야 하며 어떻게든 방법을 찾아야 합니다.

사람은 주사위를 던진다.

측정자를 동전 위에 놓는 순간 오차 \(\Delta d\) 가 결정되는 것은 맞는 말이지만, 중심점에 정확하게 놓는 것은 불가능하며 심지어는 중심점과 측정선 사이의 거리 \(l\)도 측정할 수 없으니 \(\Delta d\)를 계산해낼 수 없습니다. 그러면, 도대체 어떻게 측정오차를 추정해야하는 것일까요?

\(l\) 을 적절한 범위 내에서, 적절한 분포의 확률밀도함수를 가지는 무작위변수라고 생각합니다. 측정오차 가챠뽑기

당연히 \(l\) 의 확률밀도함수에 따라 \(\Delta d\)의 확률밀도함수가 달라집니다. \(l\) 의 확률밀도함수로부터 \(\Delta d\)의 확률밀도함수를 구하는 것은 수학적으로 유도할 수 있는 과정이지만, 계산이 길고 지루하기 때문에 보실 분만 보시기 바랍니다.

클릭하여 펼치기

분명 저는 경고했습니다.

계산의 편의성을 위해, 다음과 같이 가정합니다.

1. \(l\) 이 전 실수 구간 (음의 실수에서도) 존재할 수 있다고 가정합니다.
   • \(D\) 또한 음의 실수 \(l\)에서도 존재할 수 있습니다: \(l\) 에 대한 요소가 전부 \(l^2\)으로만 계산되기 때문입니다.
   • 단, \(D\) 의 역함수가 필요하기 때문에, 양의 \(l\) 에 대한 함수를 \(D_+\), 음의 \(l\) 에 대한 함수를 \(D_+\) 로 정의합니다.
2. \(l\)의 참값 분포 함수 \(P_l\left(l\right)\) 를 다음과 같이 가정합니다. \(P_l\left(l\right) = \mathrm{Uniform}\left[ l; -k,k\right]\)

위와 같은 가정 하에서, \(P_l\left(l\right)\) 와 \(D\left(l\right) = 2\sqrt{\left(\frac{d_0}{2}\right)^2-l^2}\) 를 통해 측정되는 참값의 분포인 \(P_D\left(D\right)\)를 알 수 있습니다.

\(P_D\left(D\right)\) 를 구하기 위해서, \(P_l\left(l\right)\) 와 \(P_D\left(D\right)\) 의 부분 누적 확률 분포 사이의 관계를 활용합니다.

\[P_l\left( \left\lbrace l | l < a \right\rbrace \right) = P_D\left( \left\lbrace D | D = D(l) \mathrm{~with~} l < a \right\rbrace \right)\]

위 식과 같이, \(l\)이 어떤 값 \(a\)보다 작을 확률은, \(l\)로부터 유도된 \(D(l)\)이, \(l < a\) 일 때의 모든 확률의 합입니다.

우리가 구하고자 하는 것은 \(P_D\left(D\right)\) 이기 때문에, 위 식을 적절히 변형하여 \(l\) 에 대해 구성되어있는 것을 \(D\)에 대해서 정리하여야 합니다. 바로 그렇게 변형해보면,

\[\require{cancel} \begin{align} \mathrm{(lhs.)} =& \xcancel{ P_l\left ( \left\lbrace l | l = D^{(-1)}\left(D\right) \mathrm{~for~} D^{(-1)}\left(D\right) < D^{(-1)}\left(b\right) \right\rbrace \right) } \\ =& ~P_l\left( \left\lbrace l | l = D^{(-1)}_{+}\left(D\right) \mathrm{~for~} D^{(-1)}_{+}\left(D\right) < D^{(-1)}_{+}\left(b\right) \right\rbrace \right. \\ &\cup \left. \left\lbrace l | l = D^{(-1)}_{-}\left(D\right) \mathrm{~for~} D^{(-1)}_{-}\left(D\right) > D^{(-1)}_{-}\left(b\right) \right\rbrace \right) \\ \mathrm{with~ }b =& D(a) \end{align}\]

이어야 합니다. 맨 앞 식이 틀리고, 집합 하나가 두개로 분리된 이유는 \(D = D(l)\) 은 일반적으로 역함수가 정의되지 못하기 때문입니다. _{앞에서도 언급한 바 있음.}

오른쪽 항은 간단해집니다. 당연히 입장을 뒤집었으니까…

\[\mathrm{(rhs.)} = P_D\left( \left\lbrace D | D < b \right\rbrace \right)\]

이제, 모든 집합식을 적분식으로 바꿔서 풀 차례입니다.

\[\mathrm{(convert~rhs.)} = \int_{0}^{b} P_D\left(D\right)dD\]

\(D\) 측정값의 최소값은 0이므로, 부분누적확률도 0부터 시작해야 합니다. 우변의 변환은 간단합니다. 좌변을 변환하면 다음과 같습니다.

\[\begin{align} \mathrm{(convert~lhs.)} = & \int_{0}^{D^{(-1)}_{+}\left(b\right)}P_l\left(l\right) dl + \int_{D^{(-1)}_{-}\left(b\right)}^{0}P_l\left(l\right) dl\\ = & \int_{D^{(-1)}_{-}\left(b\right)}^{D^{(-1)}_{+}\left(b\right)}P_l\left(l\right) dl \end{align}\]

그래서, \(\mathrm{(convert~lhs.)}\) 와 \(\mathrm{(convert~rhs.)}\) 를 같다고 놓으면,

\[\int_{0}^{b} P_D\left(D\right) dD = \int_{D^{(-1)}_{-}\left(b\right)}^{D^{(-1)}_{+}\left(b\right)}P_l\left(l\right) dl\]

로 정리됩니다. 구하고 싶은 것은 \(P_D\left(D\right)\) 였으니, 양 변을 \(b\) 에 대해서 미분해주고 \(b\) 를 \(D\) 로 직접치환하면 답이 나옵니다. 그렇게 정리하면,

\[\begin{align} P_D\left(b\right) &= \frac{d}{db}\int_{D^{(-1)}_{-}\left(b\right)}^{D^{(-1)}_{+}\left(b\right)}P_l\left(l\right) dl\\ &= P_l\left( D^{(-1)}_{+}\left(b\right) \right) \frac{d}{db} D^{(-1)}_{+}\left(b\right) - P_l\left( D^{(-1)}_{-}\left(b\right) \right) \frac{d}{db} D^{(-1)}_{-}\left(b\right) \end{align}\]

이 됩니다.

원래의 수식으로부터 이를 전부 풀기 위해, \(D^{(-1)}_{\pm}\left(D\right), \frac{d}{db} D^{(-1)}_{\pm}\left(D\right)\) 를 구하면

\[\begin{align} D_{\pm}^{\left(-1\right)}\left(b\right) &= \pm \sqrt{\left(\frac{d_0}{2}\right)^2 - \left(\frac{b}{2}\right)^2}\\ \frac{d}{db}D_{\pm}^{\left(-1\right)}\left(b\right) &= \pm \frac{b}{4 \sqrt{\left(\frac{d_0}{2}\right)^2 - \left(\frac{b}{2}\right)^2}} = \frac{b}{4D_{\pm}^\left(-1\right)\left(b\right)} \end{align}\]

이고, 이것을 활용하여 \(P_D\left(b\right)\)를 더 간단하게 하면,

\[P_D\left(b\right) = \frac{b}{4D_{+}^\left(-1\right)\left(b\right)}\left( P_l\left( D^{(-1)}_{+}\left(b\right) \right) + P_l\left( D^{(-1)}_{-}\left(b\right) \right) \right)\]

가 된다. 이 상태에서 \(P_l\) 의 제시 없이 더이상 풀 수 없으므로, \(P_l\left(l\right) = \mathrm{Uniform}\left[ l; -k,k\right]\) 을 가져옵니다.

\[P_l\left(l\right) = \left\lbrace\begin{align}\frac{1}{2k} &~~~ -k < l < k\\0 &~~~ \mathrm{otherwise.} \end{align}\right.\]

\(P_l(-l) = P_l(+l)\) 이므로, 다음과 같이 더 간단하게 \(P_l\left(l\right)\)를 정리할 수 있습니다.

\[P_D\left(b\right) = \frac{b}{2D_{+}^\left(-1\right)\left(b\right)} P_l\left( D^{(-1)}_{+}\left(b\right) \right)\]

이제, 마지막으로 \(P_l(l)\) 의 분포를 활용하여 다음과 같이 정리할 수 있습니다.

\[P_D\left(b\right) = \left\lbrace\begin{align} \frac{b}{4kD_{+}^\left(-1\right)\left(b\right)} &~~~ -k < D^{(-1)}_{+}\left(b\right) < k\\\\ 0 &~~~ \mathrm{otherwise.} \end{align}\right.\]

그래서… _{여기까지가 수식 유도의 끝입니다. 먼 길 오셨습니다.}

\(l\)의 참값 분포함수가 \(P_l\left(l\right) = \mathrm{Uniform}\left[ l; -k,k\right]\)일 때, 다음과 같이 측정값 분포함수 \(P_D\left(b\right)\)를 쓸 수 있습니다. _{참고 자료 (외부, 새 창열기)}

\[P_D\left(b\right) = \left\lbrace\begin{align} \frac{b}{4k\sqrt{\left(\frac{d_0}{2}\right)^2 - \left(\frac{b}{2}\right)^2}} &~~~ 0 < \sqrt{\left(\frac{d_0}{2}\right)^2 - \left(\frac{b}{2}\right)^2} < k\\\\ 0 &~~~\mathrm{otherwise.} \end{align}\right.\]

참고: 오차가 전도되는 과정이 간단한 함수가 아닌, 꽤 많은 요소가 적용되고 계산이 복잡해져서 해석적으로 계산하기 힘든 경우에는 몬테카를로 시뮬레이션이라는 방법으로 이런 오차 관계를 계산하게 됩니다. 꽤 이야기가 많아질테니, 다음에 다루도록 하겠습니다.

주사위만 던지면 끝인가? : From Analogue To Digital

측정자가 잘못하면 오차가 나올 수도 있다 라는 사실은 사실상 거의 모두가 알고 있었던 사실일 것입니다. 이제는… 계기의 이야기입니다.

계측 교정문제

측정자는 늘어날 수 있습니다. 온도에 의해서든, 측정자를 그간 다루던 사람이 망가뜨렸든, 아예 만들때부터 잘못되었든 측정자가 정확하지 않을 수 있습니다.

반올림 오차

아날로그를 디지털로 바꾸면, 당연히 오차가 생깁니다. 가장 간단한 예시로, 어떤 길이를 측정했을 때 그 측정값이 \(5.0\mathrm{cm}\) 라고 한다면 그 물체의 길이는 정확하게 \(5.0\mathrm{cm}\) 일까요? 당연히 정확한 \(5.0000000 ~\dddot{}~\mathrm{cm}\) 일 확률은 거의 없습니다. 어느 다른 참값으로 측정하고자 하는 어떤 양이 있지만, 측정되는 단위가 \(0.1\mathrm{cm}\) 이기 때문에, \(1.0\mathrm{cm}\) 이라는 깔끔한 숫자가 나왔을겁니다.

데이터의 참값이 \(1.02\mathrm{cm}\) 였다면, 측정값인 \(1.0\mathrm{cm}\) 와의 차이인 \(0.02\mathrm{cm}\) 가 측정 오차로 작용하게 됩니다.만약 이 거리에서 낙하한 물체의 낙하시간을 기록하여 중력가속도를 측정한다고 하면, 실제로 낙하하는 거리에 비해 측정거리가 짧으니, 중력가속도는 조금 더 크게 나오겠지요.

이렇게 계기상에 표기되는 숫자의 한계로 인해 발생하는 오차를 반올림 오차 _{Round-Off Error} 라고 합니다.

계기도 주사위를 던지는가?

한줄 요약: 네.

반올림 오차도 측정에 단순하게 적용되지 않습니다.

Q: 뭐라고요? 1의 자리에서 반올림 하면 5 이상이면 10이고, 5 미만이면 0인게 아니라고요?
A: 기계가 그걸 어떻게 알아요? 그렇게 될 거라고 측정하는 사람이 믿는거지…

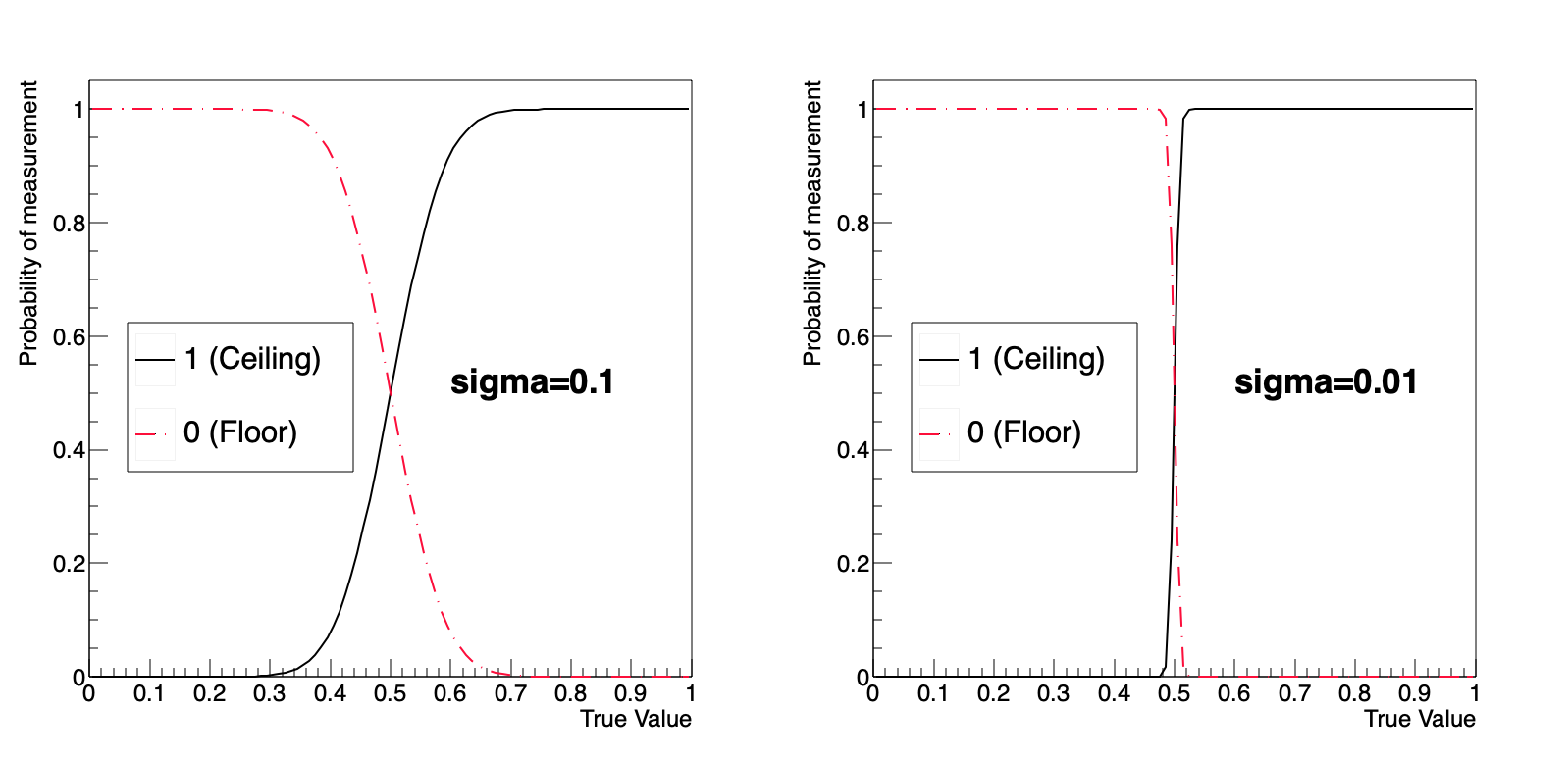
사람이 눈금으로 읽는 것이든 기계가 눈금을 읽어주는 것이든 반올림 되는 부분 인근에서는 측정의 불확정성을 보여줄 수 있습니다. 0 또는 1을 읽는 눈금이면, 참값이 0.5 부근이라면 0으로 읽을지 1로 읽을지 당연히 불분명할 것입니다. 이런 사실을 기반으로 그래프로 그리면 아래와 같은 참값에 따른 올림/버림에 대한 확률의 그래프가 나옵니다.

Go to code (gist)

그러면, 저 \(\mathrm{sigma}\)를 어떻게 구하는지가 가장 큰 문제일 것입니다. 답은… 시도해보는 수 밖에 없습니다. 시도해볼 자신이 없다면, 측정에 필요한 정확도에 맞게, 명확하게 측정해줄 수 있는 장비를 사면 됩니다. 돈이면 다 됨

요약

지금까지의 과정을 토대로 정리해보면 다음과 같습니다.

1. 실험 환경을 구성했을 때 측정값의 분포가 결정됨.
2. 실험을 진행할 때, 반올림 오차가 적용됨.

지금까지의 설명을 요약해보면 다음 그림과 같습니다.

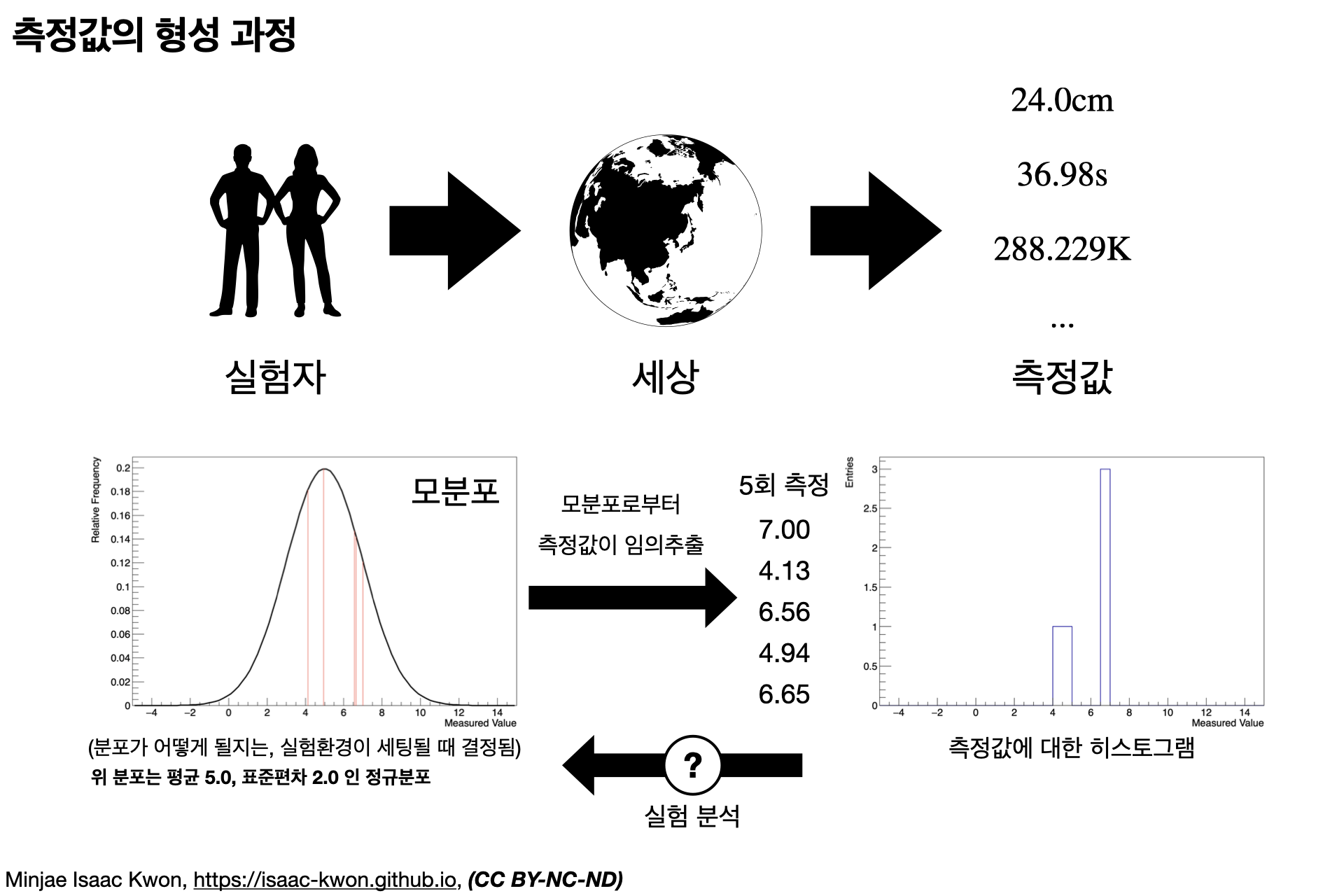
반대로 가기: Digital To Analogue

어떤 참값이 측정값으로 변환되는 과정에서 반올림 오차가 발생할 수 있다는 것은 이제 알았습니다. 그런데, 물리 현상은 참값을 기준으로 일어나기 떄문에 참값을 알아야 물리 현상을 추론할 수 있습니다. 그런데…

측정을 하면서 잃어버린 정보를 역추적하여 다시 정보를 부풀릴 수는 없습니다.

그래서, 잃어버린 정보를 다시 되돌려놓을 수는 없고, 참값의 범위 만 살려서 이 안에 어딘가에 내가 찾는 참값은 있겠지 라고 정신승리 하게됩니다. 불확도 라는 개념은 여기서 등장합니다. 그래서, \(0.1\mathrm{cm}\) 눈금으로 측정한 \(5.0\mathrm{cm}\) 측정값은 \(\left[4.95, 5.05 \right]\mathrm{cm}\) 의 범위 내에 있을 것으로 생각할 수 있고, 매번 저렇게 표기할 수는 없으니, \(5.00 \pm 0.05\mathrm{cm}\) 로 표기하여 측정값이 \(5.0\mathrm{cm}\) 이나, \(0.05\mathrm{cm}\) 만큼 위-아래로 진동할 수 있음을 나타냅니다.

참고로, \(0.1\mathrm{cm}\) 이 눈금 최소값이라 그 절반인 \(0.05\mathrm{cm}\) 를 불확도로 지정하는 것은 꽤 신빙성이 있긴 합니다만, 굳이 무조건 그렇게 할 이유는 없습니다. 만약 자기 눈이 충분이 좋아서 몽골눈 \(0.1\mathrm{cm}\) 눈금 안에서 충분이 잘게 쪼개서 어림짐작하여 볼 수 있다면 \(0.01\mathrm{cm}\) 이라고 써도 무방합니다. 대부분의 경우에는 그렇지 않기도 하고, 눈금값으로 쓰는게 안전하니 그럴 수 있습니다.

반대로, 길이 측정을 할 대상이 측정하기에 적절하지 않아서 지랄맞아서 참값에 대해 측정값의 오차가 눈금값보다 더 많이 발생할 수도 있습니다. 예를 들면, 일반적인 직자(\(15\mathrm{cm}\) 나 \(30\mathrm{cm}\) 자) 로 동전의 지름을 측정한다고 하면 자가 위치한 곳에 따라 제대로 지름을 측정할 수도 있고 그렇지 않을 수도 있습니다.

실험 통계 분석

여기서 모든 것을 설명하기에는 너무 길어지기 때문에 부연 설명은 생략하고 실험과목에서의 활용만 다룹니다.

실험 과목에서의 “동일한 값의 여러 회 측정” 을 하면 보통 아래 두가지를 가장 자주 구합니다.

• 평균
• 표준편차

그리고 측정값의 평균에 활용하는 측정 횟수가 늘어날수록, 그 평균값은 우리가 생각하는 참값에 가까워질 것라고 (직관적으로, 아주 자연스럽게) 생각합니다.

과연 그럴까요? 아니 당연하잖아

Go to code (gist)_Canvas4

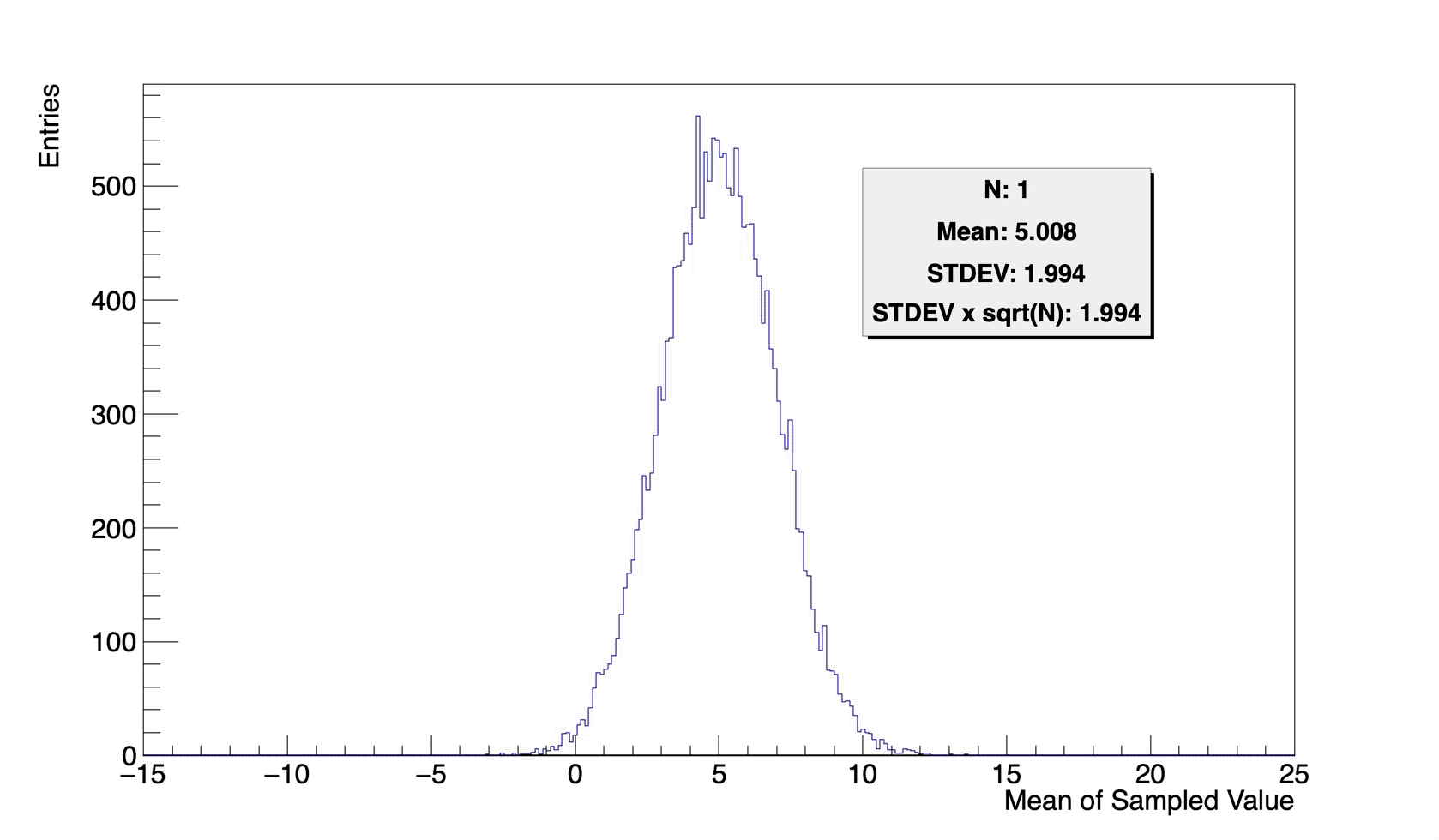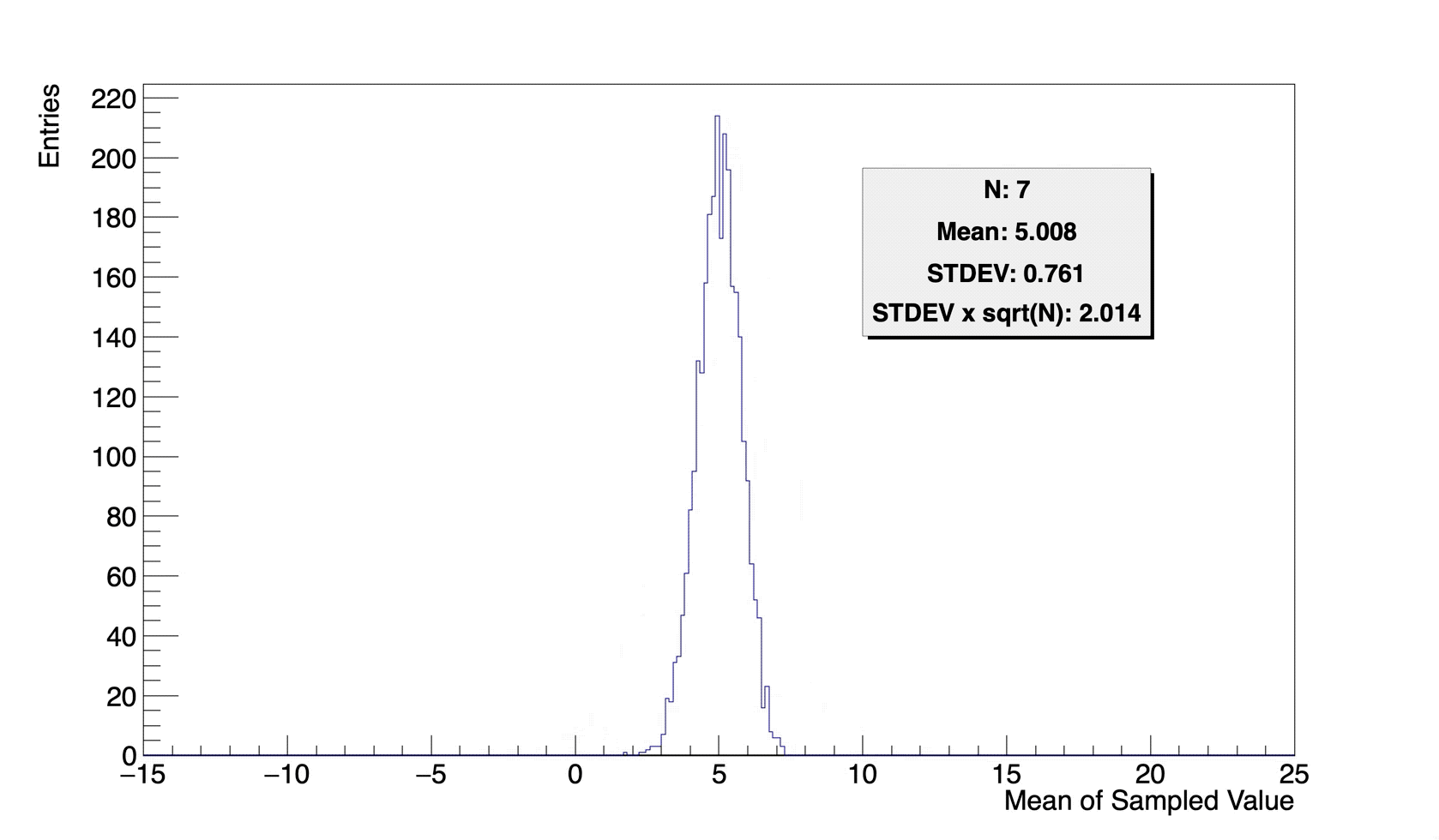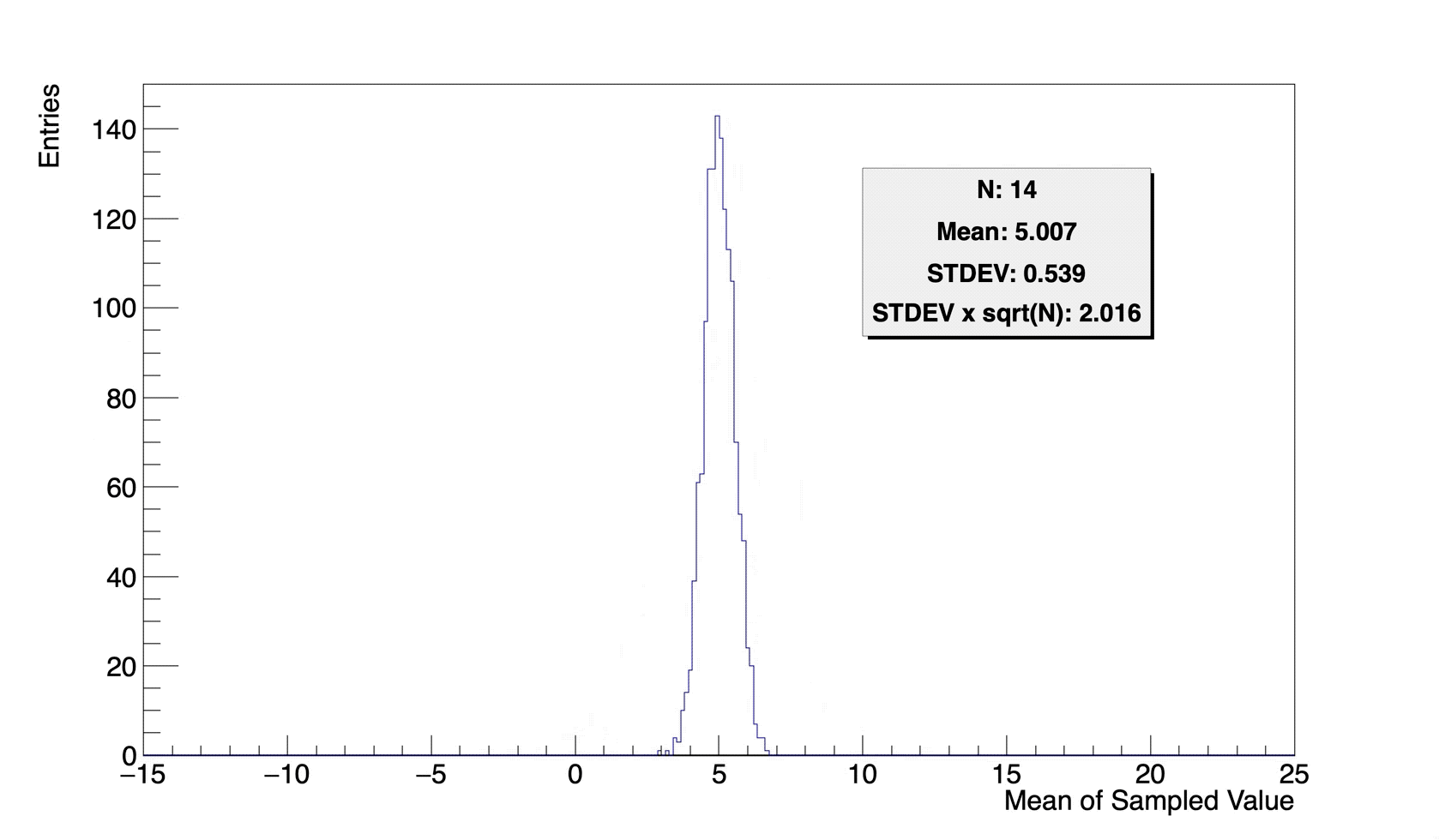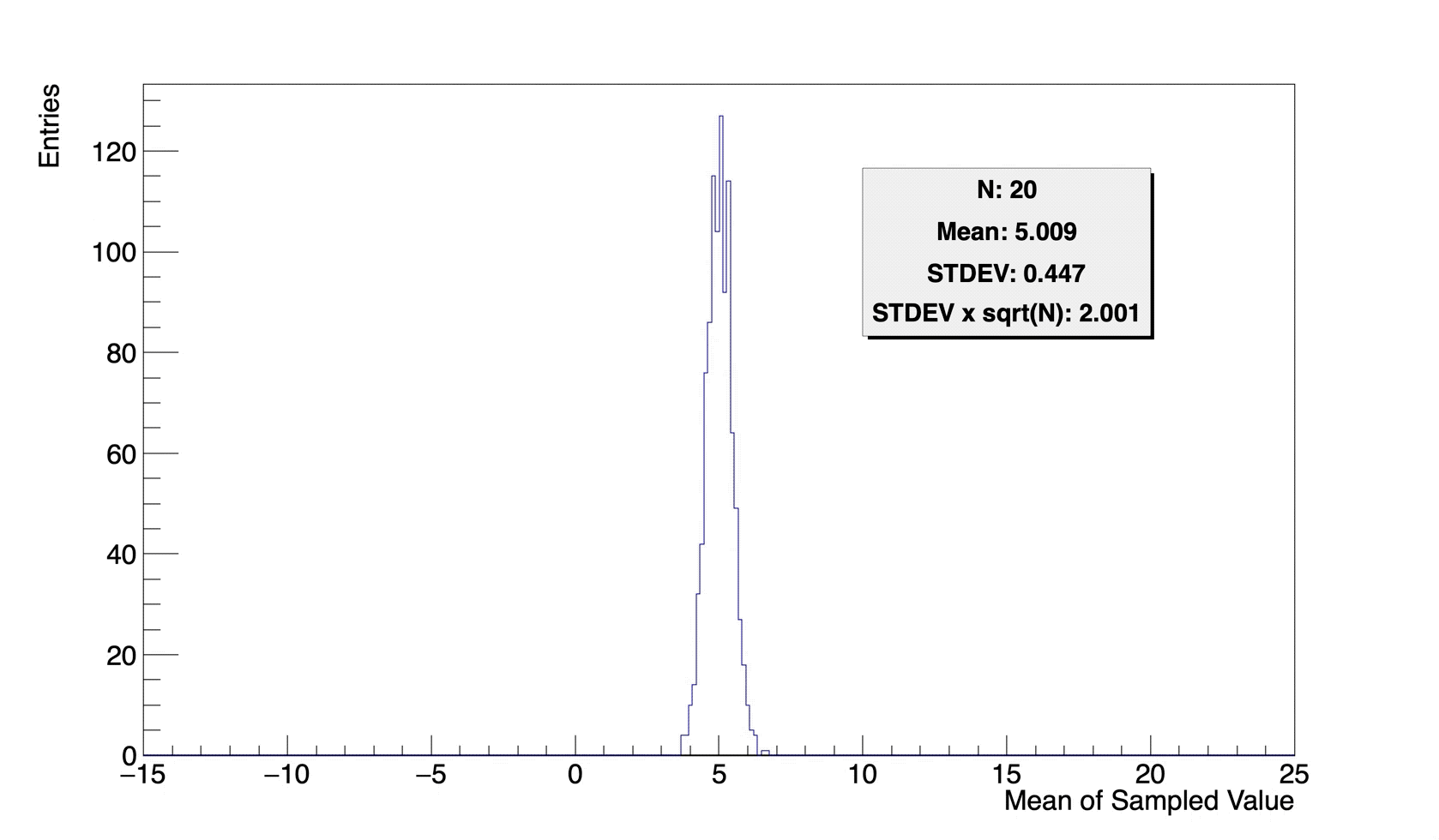
위 그림은, \(5\) 를 평균으로 하고 \(2\) 를 표준편차로 하는 정규분포를 모분포로 하는 난수 생성기로부터, \(N\)개의 실수를 무작위 추출하여 평균을 구한 것을 변량으로 하는 히스토그램입니다. (\(5\mathrm{cm}\) 가 측정값 모분포의 평균이고, \(2\mathrm{cm}\) 가 표준편차인 측정환경으로부터 측정한 값 \(N\) 개를 추출하여 평균을 취한것과 동일합니다.) 여기서의 “\(N\)개의 실수를 무작위 추출한 평균” 은 통계학에서 “표본평균” 이라고 부릅니다. 그리고 그것과 함께 구할 수 있는 표준편차는 “표본표준편차” 라고 부릅니다.

\(N\) 이 늘어남에 따른 표본평균의 분포를 살펴보면, 표본평균의 평균(그림의 Mean)은 모분포의 평균인 \(5\)로 고정되어있고, 표본평균의 표준편차(그림의 STDEV)는 \(N\) 이 증가할수록 그 값이 줄어드나, 그 값은 모분포의 표준편차인 \(2\)와 \(1/\sqrt{N}\)배 차이남을 볼 수 있습니다. 이는 중심극한정리에 의해 자명한 사실이니, 별도의 증명은 생략하도록 하겠습니다._{Wikipedia, Central Limit Theorem} 그리고, 여기서의 표본평균의 표준편차는 다른 말로 표준오차 라고도 합니다.

주의: 여기부터는 내용이 어려워집니다.

중심극한정리에 의해 측정횟수 \(N\) 을 늘리면 표본평균은 모평균이 평균이고 표준편차가 0으로 수렴하는 어떤 정규분포를 만들테니, 무한정 측정하면 길이의 참값에 접근하는 표본평균을 구해서 행복해질 수 있을까요?

이번 측정에서는 그렇지 않을 수도 있습니다. 뭐라고??

한계

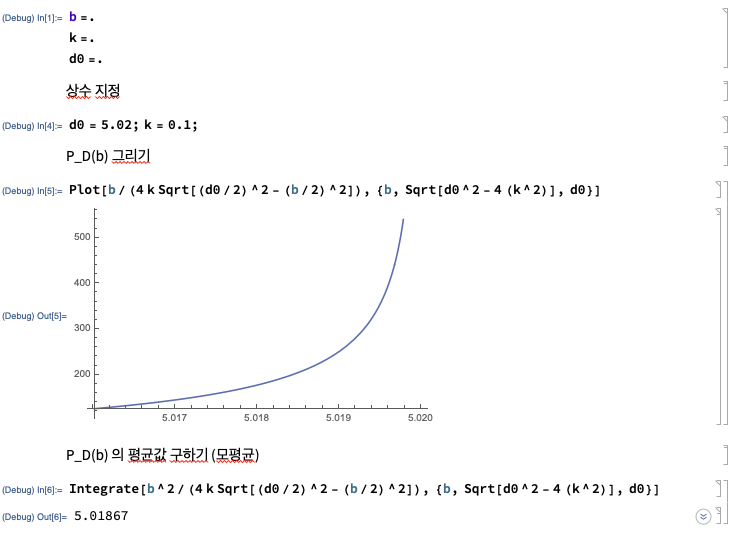
단순하게, 위의 \(P_D(b)\) 의 분포를 \(d_0 = 5.02, k=0.1\) 로 두고, 그 평균값을 Mathematica 로 구해보면 그 값이 실제 참값 지름으로 가정했던 \(d0 (=5.02)\) 가 나오지 않습니다. 당연히 측정가능한 값의 최댓값이 \(d_0\)이고 최솟값이 \(d_0\)보다 작은 값이니 평균은 그 중간의 값이여야 할 것이고, \(d_0\)가 될 수 없는 처사인 것입니다. 모평균이 \(d_0\) 와 떨어져있으니 표본평균의 평균은 \(d_0\)가 아니고, \(N\) 을 무한정 늘릴수록 \(d_0\)과는 멀리 떨어지게 됩니다. 아이고 맙소사, 우린 이제 글렀어

아직 한 발 남았다.

아직, 눈금값 오차를 고려하지 않았습니다. 위 그림에서의 적분값은 눈금값이 무한히 자세할 때에만 적용됩니다. 실제로는 \(0.1\mathrm{cm}\) 단위로 측정을 할 수 있을것이므로, 위 그래프에서 \(\left[5.016\mathrm{cm}, 5.020\mathrm{cm}\right]\) 의 범위를 가지는 측정값은 \(0.1\mathrm{cm}\) 단위의 반올림으로 모두 \(5.0\mathrm{mm}\) 으로 측정될 것이고 몇 회 측정을 하든 측정평균값은 \(5.0\mathrm{cm}\), 표준편차는 \(0.0\mathrm{cm}\) 가 되는 마법같은 결론이 나올 것입니다.

그렇다면, \(0.05\mathrm{cm}\) 이하는 구별할 수 없게되는 계통적 불확도에 들어가게 되므로, 계통적 불확도와 통계적 불확도를 동시에 작성하게 되면 다음과 같습니다.

\[5.0 \pm 0.00\mathrm{(stat.)} \pm 0.05\mathrm{(sys.)} \mathrm{~~with~} N=\mathrm{Any}\]

그런데, 만약 \(0.01\mathrm{cm}\) 까지 구별할 수 있는 측정장치를 쓴다면, 또는 \(0.001\mathrm{cm}\) 까지 구별할 수 있는 측정장치를 쓴다면 어떻게 될까요?

그러면 위 그림에서의 그래프 모양을 어느정도 측정값 분포가 따라갈 수 있게 될 것이고, 그 평균값도 \(5.0\) 이 아닌, 다른 자세한 값을 가질 수 있을 것입니다. (물론 그 값은 \(5.02\mathrm{cm}\)에 수렴하지 않습니다.)

만약, \(0.001\mathrm{cm}\) 까지 구별할 수 있는 자로 \(N=36\)회 측정하여 \(5.018\mathrm{cm}\) 의 측정평균과 \(0.030\mathrm{cm}\) 의 측정표준편차를 얻었다면 다음과 같이 표기할 수 있을 것입니다.

\[5.018 \pm 0.005\mathrm{(stat.)} \pm 0.0005\mathrm{(sys.)} \mathrm{~~with~} N=\mathrm{36}\]

보통의 경우에는, 통계적 불확도 (위의 \(\mathrm{stat.}\))와 계통적 불확도(위의 \(\mathrm{sys.}\)) 를 합성 \((\sqrt{0.005^2 + 0.05^2}=0.0502)\) 하여 표기하기 때문에,

\[5.018 \pm 0.05 \mathrm{~~with~} N=36\]

가 됩니다. 정신승리

그래서, 우리가 할 수 있는건 이게 끝인가요?

끝이겠냐

닭 잡는데 소 잡는 칼이긴 한데 측정값이 만들어지는 과정을 아주 잘 알고 있고, 그것을 어떤 방식으로든 계산으로 잘 재현할 수 있을 때, Unfolding 이라는 과정을 쓰면 측정값의 분포로부터 참값에 더 가까이 다가갈 수 있습니다. 조만간 이에 대해서 포스트를 작성해보겠지만, 그것이 언제가 될 지는…

To be continued…